A SQL query compiler from scratch in Rust (step by step): Part one, the query plan representation

One of my favorite books is Crafting Interpreters by Robert Nystrom, a very practical book that walks you through the process of building an interpreted programming language. In the same spirit, I thought it would be fun to write a series of blog spots as I go through the process of writing a new query compiler from scratch once again. After having worked in several query compilers, and written a few others for learning purposes (such as this one), I really believe in failing better every time and learning in the process. So let’s fail better together this time!

Even though I’ve been a C++ dev for more than a decade, I have chosen Rust for this journey. I have limited professional experience with Rust, but enough to appreciate how fun writing Rust is.

Writing a fully functional query compiler is a huge task. Something just too big for a pet project like this. Also, since there is no query engine this is targeted for, I will just focus on the stuff that is common to most query compilers: the SQL parser, the binder, the type system, the logical plan and the logical query rewrites. This last part is where I plan to focus more, implementing some simple query rewrites, such as predicate pushdown rewrites, and some more complex ones, such as predicate propagation through join equalities, subquery decorrelation or removing redundant join operands.

The source code of this project can be found here.

Scalar expression representation

Okay, but where do we start? The most common approach is to start with a parser that generates an AST followed by some kind of binder, planner or converter, that validates the AST and converts it into a logical or semantic plan representation. However, I will start with the logical plan representation first and how to apply transformations to it, because to me that’s where fun can be found.

In this logical plan representation we typically have logical operators that may contain scalar expressions. Let’s start with how scalar expressions are represented. For this I tend to prefer a copy-on-write representation for two reasons: minimizing memory the footprint of the query, but, more importantly, faster expression comparison as we can avoid descending some sub-expressions if the two sub-expression being compared point to the same memory region.

Rust’s enum feels like the perfect tool for the job, since we are going to need to a lot of pattern matching of expressions, so let’s use an enum for this:

enum ScalarExpr {
    Literal {
        value: String, // How to represent literal values deserves its own posts
    },
    InputRef {
        index: usize,
    },
    BinaryOp {
        op: BinaryOp,
        left: Rc<ScalarExpr>,
        right: Rc<ScalarExpr>,
    },
    NaryOp {
        op: NaryOp,
        operands: Vec<Rc<ScalarExpr>>,
    },
    ...
}

type ScalarExprRef = Rc<ScalarExpr>;

Rc is Rust’s shared pointer so to speak, and it is key for our copy-on-write approach as we will see.

Of course, this is just the initial version and we may re-visit some things as we go along. For example, the distinction between binary operations and n-ary ones feels handy for pattern matching as well, so let’s move forward with this and re-visit later if needed.

It is needless to say that BinaryOp and NaryOp are also enums.

Hopefully, in some later post we will add support for correlated column references and subqueries, but let’s jut omit that bit for now.

In this representation, all expressions within an operator are written in terms of the columns projected by their inputs, which are referenced by using InputRef expression type. This is what I call an offset-based representation, as opposed to a variable-based representation, where some operators define new variables that can be referenced by the operators upstream by their names or unique IDs. There is a good blog post from Justin Jaffray comparing both approaches (if you are into query optimizers I strongly recommend subscribing to his newsletter). If time permits, it would be a fun project to write a similar query compiler using a variable-based representation and compare the two.

Expression visitation

Once we have a representation for scalar expressions we can now write some utilities we are going to need for transforming queries. Let’s start with a simple utility: a function that given an expression collects all the columns from the input operators referenced in the expression, ie. a utility that traverses the given expression and collects all the distinct indices in all InputRefs sub-expressions. The signature of this utility function is shown below:

fn collect_input_dependencies(expr: &ScalarExprRef) -> HashSet<usize>;

We could easily implement this as a recursive function but then the possibility of overflowing the stack with a huge input query would always be there. Instead, I tend to prefer avoiding recursion as much as possible anywhere in a query compiler.

Also, instead of replicating similar code in every utility for traversing an expression, let’s implement a generic expression visitation function. In order for to be as generic as possible, this function will perform a pre-post-order visitation of the expression given and, for each sub-expression node, it will invoke the corresponding callback functions of a new ScalarExprPrePostVisitor trait.

The implementor of this trait can decide whether a given sub-expression should be descended, pruned from the visitation, or to abort the entire traversal, by returning the corresponding value from PreOrderVisitationResult. The API exposed by this visitation utility is as follows:

pub enum PreOrderVisitationResult {
    VisitInputs,
    DoNotVisitInputs,
    Abort,
}

pub trait ScalarExprPrePostVisitor {
    fn visit_pre(&mut self, expr: &ScalarExprRef) -> PreOrderVisitationResult;
    fn visit_post(&mut self, expr: &ScalarExprRef);
}

pub fn visit_scalar_expr<V>(expr: &ScalarExprRef, visitor: &mut V)
where
    V: ScalarExprPrePostVisitor;

Now let’s implement the visitation logic:

pub struct VisitationStep<V> {
    pub node: V,
    pub next_child: Option<usize>,
}

impl<V> VisitationStep<V> {
    pub fn new(node: V) -> Self {
        Self {
            node,
            next_child: None,
        }
    }
}

pub fn visit_scalar_expr<V>(expr: &ScalarExprRef, visitor: &mut V)
where
    V: ScalarExprPrePostVisitor,
{
    let mut stack = vec![VisitationStep::new(expr.clone())];
    while let Some(step) = stack.last_mut() {
        if step.next_child.is_none() {
            match visitor.visit_pre(&step.node) {
                PreOrderVisitationResult::Abort => break,
                PreOrderVisitationResult::VisitInputs => {}
                PreOrderVisitationResult::DoNotVisitInputs => {
                    visitor.visit_post(&step.node);
                    stack.pop();
                    continue;
                }
            }
            step.next_child = Some(0);
        }

        if step.next_child.unwrap() < step.node.num_inputs() {
            let input_idx = step.next_child.unwrap();
            step.next_child = Some(input_idx + 1);
            let input_expr = step.node.get_input(input_idx);
            stack.push(VisitationStep::new(input_expr));
            continue;
        }

        visitor.visit_post(&step.node);
        stack.pop();
    }
}

impl ScalarExpr {
    pub fn num_inputs(&self) -> usize {
        match self {
            ScalarExpr::Literal { .. } => 0,
            ScalarExpr::InputRef { .. } => 0,
            ScalarExpr::BinaryOp { .. } => 2,
            ScalarExpr::NaryOp { operands, .. } => operands.len(),
        }
    }

    pub fn get_input(&self, input_idx: usize) -> ScalarExprRef {
        assert!(input_idx < self.num_inputs());
        match self {
            ScalarExpr::BinaryOp { left, right, .. } => {
                if input_idx == 0 {
                    left.clone()
                } else {
                    right.clone()
                }
            }
            ScalarExpr::NaryOp { operands, .. } => operands[input_idx].clone(),
            ScalarExpr::Literal { .. } | ScalarExpr::InputRef { .. } => panic!(),
        }
    }
}

The code above uses a single stack for this pre-post order traversal of the expression tree. Each level of the stack contains the node at that level and the next child of that node that will be visited when returning to that level. Once all children of the node at the current level have been visited visit_post for the current node that is then removed from the stack.

Also, as shown above we needed to implement a couple of functions for ScalarExpr to be able to generically access the sub-expressions of a given expression: num_inputs and get_input.

Okay, now we have a generic expression traversal utility that requires implementing a trait… but what if we are only interested in the pre-order part of the traversal? In fact, that’s the most common case, so let’s write a visit_scalar_expr_pre utility on top of the one above that can just take a closure as the visitation callback:

struct ScalarExprPreVisitor<'a, F>
where
    F: FnMut(&ScalarExprRef) -> PreOrderVisitationResult,
{
    visitor: &'a mut F,
}

impl<F> ScalarExprPrePostVisitor for ScalarExprPreVisitor<'_, F>
where
    F: FnMut(&ScalarExprRef) -> PreOrderVisitationResult,
{
    fn visit_pre(&mut self, expr: &ScalarExprRef) -> PreOrderVisitationResult {
        (self.visitor)(expr)
    }
    fn visit_post(&mut self, _: &ScalarExprRef) {}
}

pub fn visit_scalar_expr_pre<F>(expr: &ScalarExprRef, visitor: &mut F)
where
    F: FnMut(&ScalarExprRef) -> PreOrderVisitationResult,
{
    let mut pre_post_visitor = ScalarExprPreVisitor { visitor };
    visit_scalar_expr(expr, &mut pre_post_visitor);
}

Now we have all the utilities we need to implement our collect_input_dependencies function in a non-recursive way:

pub fn collect_input_dependencies(expr: &ScalarExprRef) -> HashSet<usize> {
    let mut dependencies = HashSet::new();
    visit_scalar_expr_pre(expr, &mut |curr_expr: &ScalarExprRef| {
        if let ScalarExpr::InputRef { index } = **curr_expr {
            dependencies.insert(index);
        }
        PreOrderVisitationResult::VisitInputs
    });
    dependencies
}

We could make visit_scalar_expr and visit_scalar_expr_pre generic functions receiving a reference to any expression type implementing a generic trait providing these two functions. As we will see if I ever get to explaining that part, we will use other intermediate representations for scalar expressions during the optimization process, so the more generic we make all the utilities around them the better. This more generic version will look like this:

pub trait VisitableExpr {
    fn num_inputs(&self) -> usize;
    fn get_input(&self, input_idx: usize) -> Rc<Self>;
}

pub trait ExprPrePostVisitor<E: VisitableExpr> {
    fn visit_pre(&mut self, expr: &Rc<E>) -> PreOrderVisitationResult;
    fn visit_post(&mut self, expr: &Rc<E>);
}

pub fn visit_expr<E, V>(expr: &Rc<E>, visitor: &mut V)
where
    E: VisitableExpr,
    V: ExprPrePostVisitor<E>
{
    // .. same exact implementation as before
}

Expression transformation

We can also use the visitation utilities in the previous section to rewrite expressions. Let’s start with a very simple rewrite but very useful at the same time.

In several query rewrites we will need to push an expression, such as a filtering expression, down through a Project operator. A Project operator contains a vector with the expressions it projects as its output columns, so to push an expression on top of it through it we need to replace all InputRefs in the expression with the expression projected by the Project operator at that position.

Consider the following example plan where there is a filter referencing the second column projected by the input projection, which forwards the first column from its input and concatenates the second and third columns from its input:

Filter ref_1 > 0
  Project [ref_0, ref_1 || ref_2]
    ...

For pushing down the filtering expression through the projection we just need to replace ref_1 with the expression in the projection at that position, ie. ref_1 || ref_2:

Project [ref_0, ref_1 || ref_2]
  Filter ref_1 || ref_2 > 0
    ...

Let’s ignore non-deterministic projections for now (famous last words) for which the transformation above is not allowed as it may alter the results of the query.

I like to call this process as dereferencing the expression. The signature of the function implementing this rewrite is the following:

pub fn dereference_scalar_expr(expr: &ScalarExprRef, map: &Vec<ScalarExprRef>) -> ScalarExprRef;

In this copy-on-write representation for scalar expressions we tend to avoid cloning sub-expressions that are not actually modified by the rewrite. For example, any literal in the input expression will be re-used by the output expression in this rewrite.

Again, let’s build some utilities that can be re-used for other expression rewrites as well. First of all, we can add a function to clone an expression but replacing its inputs with the given ones:

impl ScalarExpr {
    pub fn clone_with_new_inputs(&self, inputs: &[ScalarExprRef]) -> ScalarExpr {
        assert!(inputs.len() == self.num_inputs());
        match self {
            ScalarExpr::BinaryOp { op, .. } => ScalarExpr::BinaryOp {
                op: op.clone(),
                left: inputs[0].clone(),
                right: inputs[1].clone(),
            },
            ScalarExpr::NaryOp { op, .. } => ScalarExpr::NaryOp {
                op: op.clone(),
                operands: inputs.to_vec(),
            },
            ScalarExpr::Literal { .. } | ScalarExpr::InputRef { .. } => panic!(),
        }
    }
}

And also, a utility function that given an expression reference and a list of possibly rewritten input sub-expressions, it creates a new cloned expression using the function above if any input was rewritten. Otherwise, it returns a reference to the original expression:

fn clone_expr_if_needed(mut expr: ScalarExprRef, new_inputs: &[ScalarExprRef]) -> ScalarExprRef {
    let num_inputs = new_inputs.len();
    assert!(num_inputs == expr.num_inputs());

    if num_inputs > 0 {
        if !(0..num_inputs)
            .map(|x| expr.get_input(x))
            .zip(new_inputs.iter())
            .all(|(original, new)| {
                &*original as *const ScalarExpr == &**new as *const ScalarExpr
            })
        {
            expr = expr.clone_with_new_inputs(new_inputs).to_ref();
        }
    }
    expr
}

Now we can implement a utility function that applies this type of copy-on-write rewrites in post-order using the utility method above, keeping the rewritten input sub-expressions for the current node as the last elements of a stack. The following post-order visitor applies a given rewrite function to each node and clones any sub-expression whose inputs have been rewritten:

struct ScalarExprRewriterPost<'a, F>
where
    F: FnMut(&ScalarExprRef) -> Option<ScalarExprRef>,
{
    stack: Vec<ScalarExprRef>,
    rewrite: &'a mut F,
}

impl<'a, F> ScalarExprRewriterPost<'a, F>
where
    F: FnMut(&ScalarExprRef) -> Option<ScalarExprRef>,
{
    fn new(rewrite: &'a mut F) -> Self {
        Self {
            stack: Vec::new(),
            rewrite,
        }
    }
}

impl<F> ScalarExprPrePostVisitor for ScalarExprRewriterPost<'_, F>
where
    F: FnMut(&ScalarExprRef) -> Option<ScalarExprRef>,
{
    fn visit_pre(&mut self, _: &ScalarExprRef) -> PreOrderVisitationResult {
        PreOrderVisitationResult::VisitInputs
    }

    fn visit_post(&mut self, expr: &ScalarExprRef) {
        let num_inputs = expr.num_inputs();
        let new_inputs = &self.stack[self.stack.len() - num_inputs..];
        let mut curr_expr = clone_expr_if_needed(expr.clone(), new_inputs);
        self.stack.truncate(self.stack.len() - num_inputs);
        if let Some(rewritten_expr) = (self.rewrite)(&curr_expr) {
            curr_expr = rewritten_expr;
        }
        self.stack.push(curr_expr);
    }
}

Again, let’s write a function that can take a closure with the rewrite function:

pub fn rewrite_scalar_expr_post<F>(rewrite: &mut F, expr: &ScalarExprRef) -> ScalarExprRef
where
    F: FnMut(&ScalarExprRef) -> Option<ScalarExprRef>,
{
    let mut visitor = ScalarExprRewriterPost::new(rewrite);
    visit_scalar_expr(expr, &mut visitor);
    assert!(visitor.stack.len() == 1);
    visitor.stack.into_iter().next().unwrap()
}

Finally, our dereference_scalar_expr function could be implemented as follows:

pub fn dereference_scalar_expr(expr: &ScalarExprRef, map: &Vec<ScalarExprRef>) -> ScalarExprRef {
    rewrite_scalar_expr_post(
        &mut |expr: &ScalarExprRef| {
            if let ScalarExpr::InputRef { index } = expr.as_ref() {
                return Some(map[*index].clone());
            }
            None
        },
        expr,
    )
}

Another very common expression transformation is the opposite one, instead of pushing an expression down through a projection, it lifts the expression through the projection. Given an expression written in terms of the input of the projection, it will rewrite it in terms of the output of the projection, if possible.

The following example illustrates the effect of this rewrite, where a filtering expression is lifted up through a projection operator:

• Before:

Project [ref_0 + ref_1]
  Filter ref_0 + ref_1 > 0
    ...

• After:

Filter ref_0 > 0
  Project [ref_0 + ref_1]
    ...

However, the filter in the example below cannot be lifted through the projection since the projection doesn’t have a column exposing either the result of either ref_0 + ref_1 > 0, ref_0 + ref_1 or both ref_0 and ref_1. It does expose ref_0 as its first column, but not ref_1.

Project [ref_0]
  Filter ref_0 + ref_1 > 0
    ...

Given the examples above, we know this rewrite must be applied in pre-order since we need to find the longest sub-expression in the given expression projected by the projection operator. Also, we know that this rewrite may fail if an InputRef expression not projected by the given projection operator is reached.

The signature of this rewrite will be the following:

pub fn lift_scalar_expr(expr: &ScalarExprRef, proj: &Vec<ScalarExprRef>) -> Option<ScalarExprRef>;

where None is returned if the expression could not be lifted through the given vector of expressions.

We can easily write another utility visitor and a function to apply a rewrite closure in pre-order while cloning sub-expression only if strictly needed in post-order. The code for this could be as follows:

struct ScalarExprRewriterPre<'a, F>
where
    F: FnMut(&ScalarExprRef) -> Result<Option<ScalarExprRef>, ()>,
{
    stack: Vec<ScalarExprRef>,
    rewrite: &'a mut F,
    skip_post: bool,
}

impl<'a, F> ScalarExprRewriterPre<'a, F>
where
    F: FnMut(&ScalarExprRef) -> Result<Option<ScalarExprRef>, ()>,
{
    fn new(rewrite: &'a mut F) -> Self {
        Self {
            stack: Vec::new(),
            rewrite,
            skip_post: false,
        }
    }
}

impl<F> ScalarExprPrePostVisitor for ScalarExprRewriterPre<'_, F>
where
    F: FnMut(&ScalarExprRef) -> Result<Option<ScalarExprRef>, ()>,
{
    fn visit_pre(&mut self, expr: &ScalarExprRef) -> PreOrderVisitationResult {
        match (self.rewrite)(expr) {
            Ok(Some(rewritten_expr)) => {
                self.stack.push(rewritten_expr);
                self.skip_post = true;
                PreOrderVisitationResult::DoNotVisitInputs
            }
            Ok(None) => PreOrderVisitationResult::VisitInputs,
            Err(_) => {
                self.stack.clear();
                PreOrderVisitationResult::Abort
            }
        }
    }

    fn visit_post(&mut self, expr: &ScalarExprRef) {
        if self.skip_post {
            // `visit_pre` already left a rewritten expression in the stack
            self.skip_post = false;
            return;
        }
        // Clone the current node if needed
        let num_inputs = expr.num_inputs();
        let new_inputs = &self.stack[self.stack.len() - num_inputs..];
        let curr_expr = clone_expr_if_needed(expr.clone(), new_inputs);
        self.stack.truncate(self.stack.len() - num_inputs);
        self.stack.push(curr_expr);
    }
}

Finally, our rewrite utility for lifting expressions through a projection:

pub fn lift_scalar_expr(expr: &ScalarExprRef, proj: &Vec<ScalarExprRef>) -> Option<ScalarExprRef> {
    rewrite_scalar_expr_pre(
        &mut |expr: &ScalarExprRef| {
            if let Some(proj_col) = proj
                .iter()
                .enumerate()
                .find(|(_, proj_expr)| **proj_expr == *expr)
                .map(|(i, _)| i)
            {
                return Ok(Some(ScalarExpr::input_ref(proj_col).to_ref()));
            }
            if let ScalarExpr::InputRef { .. } = expr.as_ref() {
                Err(())
            } else {
                Ok(None)
            }
        },
        expr,
    )
}

Ok(Some(...)) indicates the given sub-expression has been rewritten. Ok(None) indicates that the given sub-expression was not rewritten but that their inputs should be descended. Err(()) indicates that the given sub-expression could not be rewritten and that the rewrite process must be aborted.

Another interesting and common expression rewrite that may also fail is re-mapping the indices of the InputRefs sub-expressions in the given input expressions:

pub fn apply_column_map(
    expr: &ScalarExprRef,
    column_map: &HashMap<usize, usize>,
) -> Option<ScalarExprRef> {
    rewrite_scalar_expr_pre(
        &mut |expr: &ScalarExprRef| {
            if let ScalarExpr::InputRef { index } = expr.as_ref() {
                if let Some(mapped_index) = column_map.get(index) {
                    Ok(Some(ScalarExpr::input_ref(*mapped_index).to_ref()))
                } else {
                    Err(())
                }
            } else {
                Ok(None)
            }
        },
        expr,
    )
}

These new rewrite_scalar_expr_post and rewrite_scalar_expr_pre utilities will be used later for all sort of expression rewrites we may need for optimizing our query plans.

Again, we could make them generic utilities that could be reused for any expression type implementing clone_with_new_inputs function through the following trait:

pub trait RewritableExpr: Sized + VisitableExpr {
    fn clone_with_new_inputs(&self, inputs: &[Rc<Self>]) -> Rc<Self>;
}

Equivalence classes

When dealing with expression in a query compiler, it is often useful to group expressions within the same context (meaning expressions written in terms of the output of the same input operators) that are known to always lead to the same values.

For instance, in the sub-plan below we know that ref_0 and 'hello' literal are equivalent expressions, so we could replace ref_0 in the output of the projection with 'hello'.

Project [ref_0, ref1]
  Filter ref_0 = 'hello'
    ...

The resulting plan would look like this:

Project ['hello', ref_1]
  Filter ref_0 = 'hello'
    ...

For this type of optimizations we need to, given a list of predicates that are known to be true, because they have been enforced earlier in the plan, group the expressions that are known to be equivalent by using only the equality predicates. We use the following data structure for grouping expressions that are known to be equivalent. We call these groups equivalence classes.

pub struct EquivalenceClass {
    /// Indicates that any of the equality predicates that lead to this class
    /// was using the null-rejecting equality operator, ie. the SQL equality
    /// operator (`BinaryOp::Eq`), and hence, none of the expressions within the
    /// class will evaluate to NULL.
    pub null_rejecting: bool,
    /// The list of expressions belonging to the class.
    pub members: BTreeSet<ScalarExprRef>,
}

pub type EquivalenceClasses = Vec<EquivalenceClass>;

null_rejecting indicates that one of the equality predicates that led to the creation of the class is the SQL equality operator, which rejects NULL values, as opposed to IS NOT DISTINCT FROM operator where two NULL values evaluate as equal.

The following two utility functions are used to work with equivalence classes. The first one computes the equivalence classes given a list of predicates, while the second one returns the equivalence class the given expression belongs to, if any.

pub fn extract_equivalence_classes(predicates: &Vec<ScalarExprRef>) -> EquivalenceClasses;

pub fn find_class(classes: &EquivalenceClasses, expr: &ScalarExprRef) -> Option<usize>;

At this point we have covered all the main concepts in the scalar_expr module in our project. Now that we know how scalar expressions are represented and how to work them, let’s dive into the core of the plan representation: the Query Graph.

The Query Graph

The copy-on-write approach we have used for scalar expression works well for trees, but unfortunately for us, queries are not trees but DAGs, for example for modeling common table expressions, either explicit ones or discovered at optimization time.

Applying rewrite rules to a DAG needs some special care as we must never modify a shared node, ie. a node reachable from more than one path from the root, using information that is only valid from one of the paths reaching it.

Consider the following DAG with a diamond shape:

   U
  / \
 F   |
  \ /
   A
   |
   T 

If filter F only references columns corresponding to grouping key items from aggregate A then we could transpose them. However, we cannot just change the input of A to point to the filter, as that would lead to the following query graph where the filter is applied in both branches of the top level union, even though in the original plan it was only applied in one of them:

   U
  / \
  \ /
   A
   |
   F'
   |
   T 

Instead, we could create a clone of A and add the filter pushed down under it, which would lead to the following valid plan, that is semantically equivalent to the initial one:

   U
  / \
 A'  A
 |   |
 F'  |
  \ /
   T 

In this section we are going to try to design a DAG representation for query plans where wrong result issues like the one above are hard to introduce.

Another issue we need to take into account in our design is how to make the borrow checker happy. Working with graph data structures in Rust is not particularly easy because of the borrow checker, specially if backpointers are needed (ie. for, given a node, easily knowing what are the parent nodes it can be reached from). Using RefCell and Rc just moves the problem to the execution time. For this, the simplest solution I’ve found is to move the ownership of the nodes of the graph to the data structure representing the graph itself.

Finally, sometimes when applying transformations, as it will happen in our query rewriter, we need to easily detect whether the query has settled in a fix point to which no more transformations can be applied. For this it is very helpful to have some kind of generation number that keeps track of the number of mutations the query graph has suffered.

The snippet below shows the representation we have chosen for our query graph. As mentioned earlier, all the nodes are owned by the query graph. They are uniquely identified and are referenced through their IDs.

pub type NodeId = usize;

pub enum QueryNode {
    Project {
        outputs: Vec<ScalarExprRef>,
        input: NodeId,
    },
    Filter {
        conditions: Vec<ScalarExprRef>,
        input: NodeId,
    },
    TableScan {
        table_id: usize,
        num_columns: usize,
    },
    Join {
        conditions: Vec<ScalarExprRef>,
        left: NodeId,
        right: NodeId,
    },
    Aggregate {
        group_key: BTreeSet<usize>,
        input: NodeId,
    },
    ...
}

pub struct QueryGraph {
    nodes: HashMap<NodeId, QueryNode>,
    entry_node: NodeId,
    next_node_id: usize,
    parents: HashMap<NodeId, BTreeSet<NodeId>>,
    pub gen_number: usize,
}

Accessing a node given its ID can be done by using the following function:

impl QueryGraph {
    pub fn node(&self, node_id: NodeId) -> &QueryNode {
        self.nodes.get(&node_id).unwrap()
    }
}

Note that the function above will panic if an invalid NodeId is passed.

Nodes are instances of our QueryNode enum. Note that we will add more node types later for modeling the remaining relation operations. Also, some of the operators are missing some members that will be added later such as the join type or the aggregate expressions.

Each node type contains members for the attributes of the node and the inputs of the node. By putting the inputs on each node type we ensure each node type always has the correct number of inputs.

However, since each node may have an unlimited number of parent nodes we have chosen to track these backpointers in a map in the QueryGraph structure. That forces us to keep this map up to date when adding and removing nodes. When adding a node we just need to register the new node as the parent of its inputs:

impl QueryGraph {
    pub fn add_node(&mut self, node: QueryNode) -> NodeId {
        let node_id = self.next_node_id;
        for i in 0..node.num_inputs() {
            self.parents
                .entry(node.get_input(i))
                .or_insert_with(|| BTreeSet::new())
                .insert(node_id);
        }
        self.next_node_id += 1;
        self.nodes.insert(node_id, node);
        node_id
    }
}

In our model, nodes are only removed via replacements, ie. a node cannot be removed but replaced with another node. Replacing a node means making all parents of the node being replaced point to the given new node. In order to replace a node the following function must be used:

impl QueryGraph {
    pub fn replace_node(&mut self, node_id: NodeId, new_node_id: NodeId) {
        // All the parents of the old node are now parents of the new one
        if let Some(parents) = self.parents.remove(&node_id) {
            for parent_id in parents.iter() {
                let parent_node = self.nodes.get_mut(&parent_id).unwrap();
                for input in 0..parent_node.num_inputs() {
                    if parent_node.get_input(input) == node_id {
                        parent_node.set_input(input, new_node_id);
                    }
                }
            }

            if let Some(new_node_parents) = self.parents.get_mut(&new_node_id) {
                new_node_parents.extend(parents);
            } else {
                self.parents.insert(new_node_id, parents);
            }
        }
        // Replace the reference to the entry node as well
        if self.entry_node == node_id {
            self.entry_node = new_node_id;
        }

        self.remove_detached_nodes(node_id);
        self.gen_number += 1;
    }
}

As shown above, every time a node is replaced the generation number of the query graph is increased keeping track of the number of modifications the query graph has gone through. This will be very handy for determining whether a query graph has settled in a fix point when applying query rewrites.

remove_detached_nodes is our way of keeping the graph as clean as possible, by removing any node under the node being replaced that is no longer reachable from the query graph. At the point where remove_detached_nodes is called the node pointed by node_id is no longer attached to the query graph as it doesn’t have any parents leading to it, so it can be removed. If any of its inputs ends up without any parent node after removing node_id node, then we could remove that input node as well. We can keep repeating this process until we reach a leaf node or a node that has another parent.

We will see later that there are some transformations that need to look for common properties among all the parents of a given node. Ensuring that all the parents of a node are actually attached to the query graph is handy for the effectiveness of these transformation rules.

Traversing the Query Graph

For traversing a query graph we can define the same utilities we had for expressions, but this time, the reference to the current node being visited is represented by the query graph and the ID of the node.

pub trait QueryGraphPrePostVisitor {
    fn visit_pre(&mut self, query_graph: &QueryGraph, node_id: NodeId) -> PreOrderVisitationResult;
    fn visit_post(&mut self, query_graph: &QueryGraph, node_id: NodeId);
}

impl QueryGraph {
    pub fn visit<V>(&self, visitor: &mut V)
    where
        V: QueryGraphPrePostVisitor,
    {
        self.visit_subgraph(visitor, self.entry_node);
    }

    pub fn visit_pre<F>(&self, visitor: &mut F)
    where
        F: FnMut(&QueryGraph, NodeId) -> PreOrderVisitationResult,
    {
        let mut pre_post_visitor = QueryGraphPreVisitor { visitor };
        self.visit(&mut pre_post_visitor);
    }

    pub fn visit_subgraph<V>(&self, visitor: &mut V, node_id: NodeId)
    where
        V: QueryGraphPrePostVisitor,
    {
        let mut stack = vec![VisitationStep::new(node_id)];
        while let Some(step) = stack.last_mut() {
            if step.next_child.is_none() {
                match visitor.visit_pre(self, step.node) {
                    PreOrderVisitationResult::Abort => break,
                    PreOrderVisitationResult::VisitInputs => {}
                    PreOrderVisitationResult::DoNotVisitInputs => {
                        visitor.visit_post(self, step.node);
                        stack.pop();
                        continue;
                    }
                }
                step.next_child = Some(0);
            }

            let node = self.node(step.node);
            if step.next_child.unwrap() < node.num_inputs() {
                let input_idx = step.next_child.unwrap();
                step.next_child = Some(input_idx + 1);
                stack.push(VisitationStep::new(node.get_input(input_idx)));
                continue;
            }

            visitor.visit_post(self, step.node);
            stack.pop();
        }
    }
}

Again, we need implement two functions, num_inputs and get_input for QueryNode so that we can traverse the query graph iteratively:

impl QueryNode {
    pub fn num_inputs(&self) -> usize {
        match self {
            Self::Project { .. } | Self::Filter { .. } | Self::Aggregate { .. } => 1,
            Self::TableScan { .. } => 0,
            Self::Join { .. } => 2,
        }
    }

    pub fn get_input(&self, input_idx: usize) -> NodeId {
        assert!(input_idx < self.num_inputs());

        match self {
            Self::Project { input, .. }
            | Self::Filter { input, .. }
            | Self::Aggregate { input, .. } => *input,
            Self::TableScan { .. } => panic!(),
            Self::Join { left, right, .. } => {
                if input_idx == 0 {
                    *left
                } else {
                    *right
                }
            }
        }
    }
}

Note that visit_subgraph visits shared nodes multiple times. The implementor of the visitor trait is responsible for implementing the logic in visit_pre to avoid descending nodes more than once if needed.

Attaching computed properties to the Query Graph

There are a lot of properties that can be computed from a query graph that can be used for optimizing it. For example, given an aggregate node whose grouping key is known to include a unique key of the input relation/node of the aggregate, we can remove the aggregate node replacing it with a projection with the constant-folded values of the aggregate expressions. Computing the unique keys of a given node usually requires computing the unique keys of its input nodes, leading to some expensive recursive computation, making this kind of optimizations very expensive unless we somehow avoid re-computing these properties unless it is strictly needed by caching them in the query graph, as we have done.

To illustrate the caching mechanism for this properties in our design let’s use the most basic derived property I can think of: the number of columns projected by a given node, ie. its arity. The following snipped shows the code we would need to execute every time we want to know the arity of a given node:

impl QueryNode {
    pub fn num_columns(&self, query_graph: &QueryGraph) -> usize {
        match self {
            Self::Project { outputs, .. } => outputs.len(),
            Self::Filter { input, .. } => query_graph.node(*input).num_columns(query_graph),
            Self::TableScan { num_columns, .. } => *num_columns,
            Self::Join { left, right, .. } => {
                query_graph.node(*left).num_columns(query_graph)
                    + query_graph.node(*right).num_columns(query_graph)
            }
            Self::Aggregate { group_key, .. } => group_key.len(),
        }
    }
}

In the worst case, the recursion stack for computing the number of columns recursively is as deep as the query graph. Less than ideal in a query compiler.

Instead, let’s add a cache of computed properties that are evaluated lazily. For this, we can add a new member to our QueryGraph structure:

pub struct QueryGraph {
    // ...
    pub property_cache: RefCell<PropertyCache>,
}

pub struct PropertyCache {
    /// Properties computed in a bottom-up manner.
    bottom_up_properties: HashMap<NodeId, HashMap<TypeId, Box<dyn Any>>>,
}

For each node, it may hold a set of properties identified by some TypeId. These properties must be invalidated whenever there is a node replacement under a given node.

As shown below, there is a free function to access each property for a given node (num_columns in this case). Internally, it uses a graph visitor to compute the property in a bottom-up manner, which avoids descending a sub-graph if the value of the property is already known for the root node of that sub-graph. num_columns_unchecked assumes the value of the property for the given node is already in the cache, as it is guaranteed by the visitation logic.

compute_num_columns_for_node is the where the property is actually computed for a given node assuming the value of the property is known for all its inputs. In fact, everything else is boilerplate code that will be the same for all bottom-up properties. We will refactor that later.

pub fn num_columns(query_graph: &QueryGraph, node_id: NodeId) -> usize {
    NumColumns::num_columns(query_graph, node_id)
}

struct NumColumns {}

impl NumColumns {
    fn num_columns(query_graph: &QueryGraph, node_id: NodeId) -> usize {
        let mut visitor = NumColumns {};
        query_graph.visit_subgraph(&mut visitor, node_id);
        visitor.num_columns_unchecked(query_graph, node_id)
    }

    fn num_columns_unchecked(&self, query_graph: &QueryGraph, node_id: NodeId) -> usize {
        query_graph
            .property_cache
            .borrow_mut()
            .node_bottom_up_properties(node_id)
            .get(&Self::metadata_type_id())
            .unwrap()
            .downcast_ref::<usize>()
            .unwrap()
            .clone()
    }

    fn metadata_type_id() -> TypeId {
        TypeId::of::<Self>()
    }

    fn compute_num_columns_for_node(&self, query_graph: &QueryGraph, node_id: NodeId) -> usize {
        match query_graph.node(node_id) {
            QueryNode::Project { outputs, .. } => outputs.len(),
            QueryNode::Filter { input, .. } => self.num_columns_unchecked(query_graph, *input),
            QueryNode::TableScan { num_columns, .. } => *num_columns,
            QueryNode::Join {
                left,
                right,
                ..
            } => {
                let left_columns = self.num_columns_unchecked(query_graph, *left);
                let right_columns = self.num_columns_unchecked(query_graph, *right);
                left_columns + right_columns
            }
            QueryNode::Aggregate {
                group_key,
                ..
            } => group_key.len(),
        }
    }
}

impl QueryGraphPrePostVisitor for NumColumns {
    fn visit_pre(&mut self, query_graph: &QueryGraph, node_id: NodeId) -> PreOrderVisitationResult {
        if query_graph
            .property_cache
            .borrow_mut()
            .node_bottom_up_properties(node_id)
            .contains_key(&Self::metadata_type_id())
        {
            PreOrderVisitationResult::DoNotVisitInputs
        } else {
            PreOrderVisitationResult::VisitInputs
        }
    }

    fn visit_post(&mut self, query_graph: &QueryGraph, node_id: NodeId) {
        if !query_graph
            .property_cache
            .borrow_mut()
            .node_bottom_up_properties(node_id)
            .contains_key(&Self::metadata_type_id())
        {
            let num_columns = self.compute_num_columns_for_node(query_graph, node_id);
            query_graph
                .property_cache
                .borrow_mut()
                .node_bottom_up_properties(node_id)
                .insert(Self::metadata_type_id(), Box::new(num_columns));
        }
    }
}

We could add some logic in visit_pre to avoid visiting the inputs of nodes whose arity can be known from the node itself, for example for Project and Aggregate, but for now let’s leave the boilerplate code as generic as possible.

The same approach can be used for computing other bottom-up properties such as the unique keys or keys with known bounds, the predicates/constraints that are known to be true at the output of a given node and many more.

Since these properties are computed from the values of the property of its inputs, it must be invalidated when there is any node replacement anywhere under a given node. The value of num_columns for a given node must never change, but other properties like the ones mentioned above may change. In order to make this mechanism as generic as possible so it works with all computed properties, we must always invalidate the cached properties for a given node if there is a node replacement anywhere under it. That can be achieved by adding some logic in the single function to perform node replacements: QueryGraph::replace_node. As shown below, we traverse the plan upwards removing the cached properties for all the nodes upstream.

impl QueryGraph {
    pub fn replace_node(&mut self, node_id: NodeId, new_node_id: NodeId) {
        self.invalidate_properties_upwards(node_id);
        ...
    }

    fn invalidate_properties_upwards(&mut self, node_id: NodeId) {
        let mut stack = vec![node_id];
        while let Some(current_id) = stack.pop() {
            let prev_size = stack.len();
            if let Some(parents) = self.parents.get(&current_id) {
                stack.extend(parents.iter());
            }

            for idx in prev_size..stack.len() {
                self.invalidate_node_properties(stack[idx]);
            }
        }
    }

    fn invalidate_node_properties(&mut self, node_id: NodeId) {
        self.property_cache
            .borrow_mut()
            .invalidate_node_properties(node_id)
    }
}

impl PropertyCache {
    pub fn invalidate_node_properties(&mut self, node_id: NodeId) {
        self.bottom_up_properties.remove(&node_id);
    }
}

Our first Rewrite Rule

In order to illustrate how to work with this representation, let’s write the simplest possible transformation rule: fusing two chained Filter operators into a single Filter operator, ie. given a Filter operator whose input is another Filter operator replace the upper one with a new Filter node containing the condition expressions from both.

First of all, let’s define the interface for implementing this basic rewrite rules:

pub enum OptRuleType {
    Always,
    TopDown,
    BottomUp,
}

pub trait SingleReplacementRule {
    fn rule_type(&self) -> OptRuleType;

    fn apply(&self, query_graph: &mut QueryGraph, node_id: NodeId) -> Option<NodeId>;
}

As we will see later, we want to apply several rewrite rules while traversing the query graph, mutating the shape of the graph. For each node visited, we want to try out a set of different rewrite rules, that may result in the replacement of one or several nodes in the graph. The trait above only covers rules that may result in the replacement of the current node being visited. When talking about column pruning for joins while preserving the DAG shape of the plan we will introduce a more generic trait for rules that may result in the replacement of more than one node.

These rules can be applied either during the top-down part of the traversal of the graph, during the bottom-up part or in both. That desire is indicated with the rule_type function.

pub struct FilterMergeRule {}

impl SingleReplacementRule for FilterMergeRule {
    fn rule_type(&self) -> OptRuleType {
        OptRuleType::TopDown
    }

    fn apply(&self, query_graph: &mut QueryGraph, node_id: NodeId) -> Option<NodeId> {
        if let QueryNode::Filter { conditions, input } = query_graph.node(node_id) {
            if let QueryNode::Filter {
                conditions: child_conditions,
                input: child_input,
            } = query_graph.node(*input)
            {
                return Some(
                    query_graph.add_node(QueryNode::Filter {
                        input: *child_input,
                        conditions: conditions
                            .clone()
                            .into_iter()
                            .chain(child_conditions.clone().into_iter())
                            .collect(),
                    }),
                );
            }
        }
        None
    }
}

In the following posts we will see how we can implement rules that replace several nodes in the query graph at once, and also, how we can apply several rules in a single pre-post-order traversal of the graph, using our visitation utility, until a fix point is reached.

Visualizing the Query Graph

Throughout the posts in this series, we will use the following visual representation for reasoning about query graphs, where each node represents a logical operator connected via directed arrows to their input nodes.

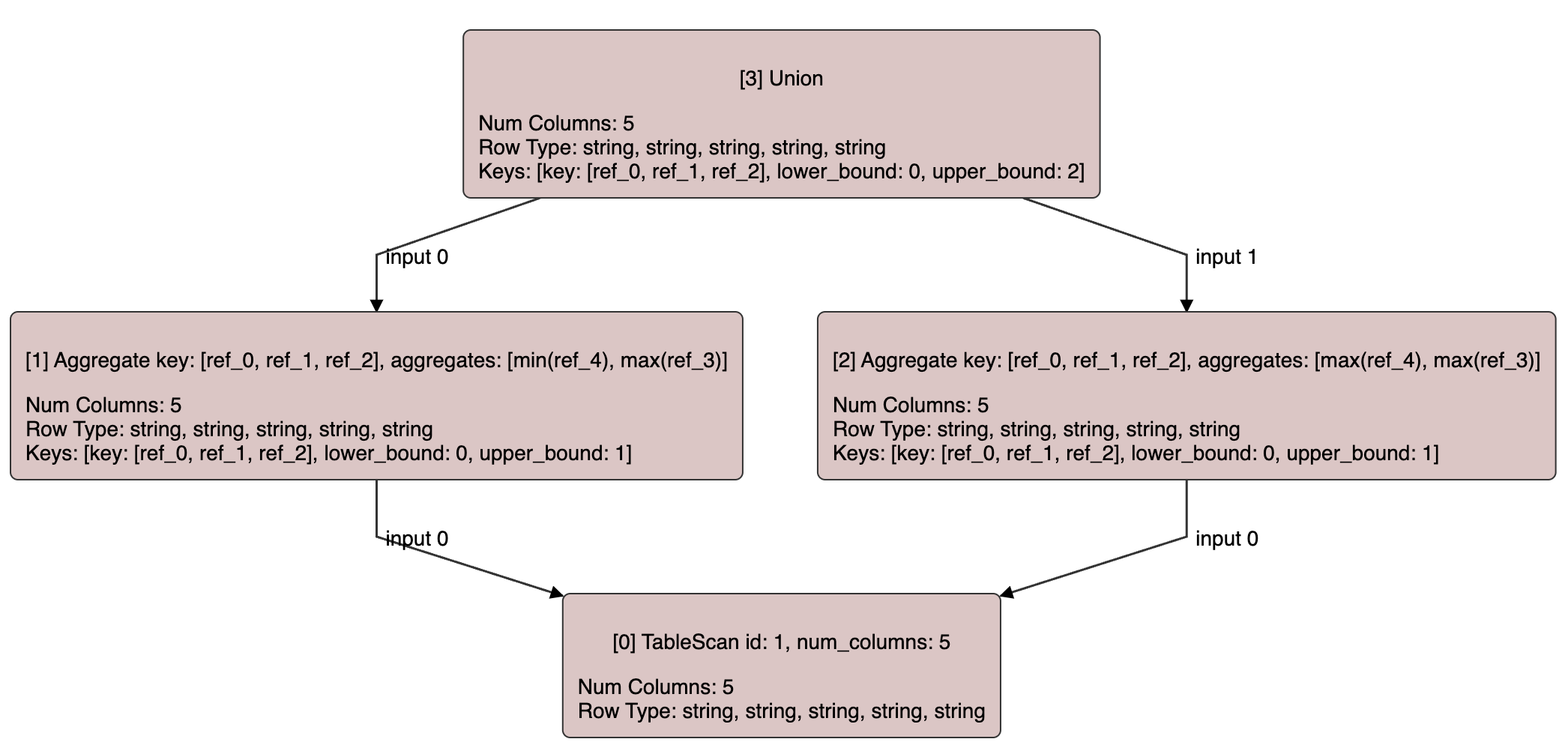
Within each node, the first line contains the unique ID of the node and its type, together with its internal properties. The remaining lines contain the computed properties for that node.

The effect of the rewrite rules can also be visualized with this representation by adding extra arrows for the node replacements. For example, the following graph shows the replacement of node 2 with node 5 that combines the filter expressions in 1 and 2, using the FilterMergeRule described earlier.

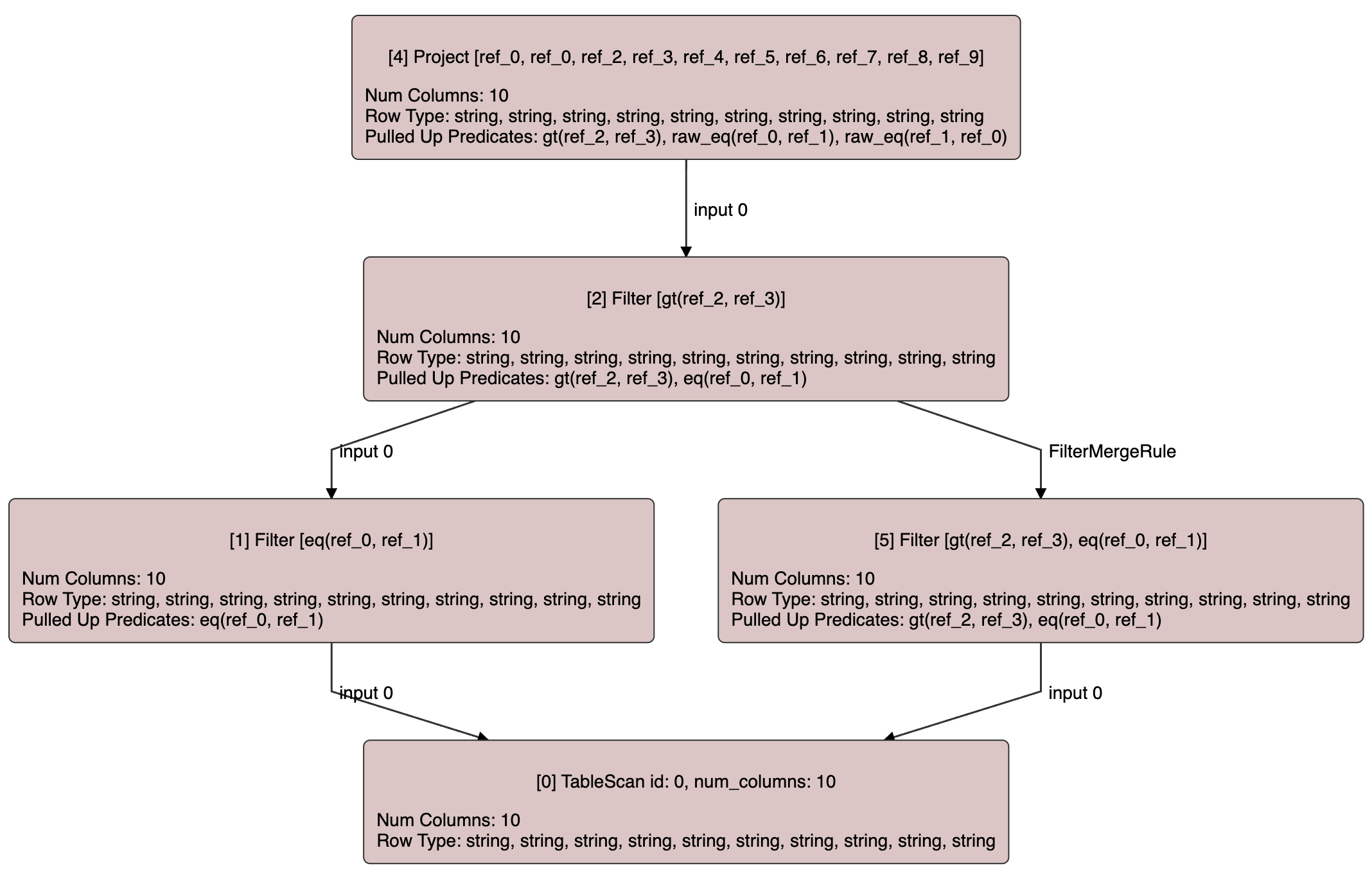
The graphs are generated from the JSON representation of the query graph and rendered using javascript.

Our first predicate pushdown rule

In this model, predicate pushdown is implemented as a set of atomic transformations. For example, one of these rules could transpose a Filter and a Project operator, using the dereference_scalar_expr we saw earlier. Its implementation is as simple as this:

pub struct FilterProjectTransposeRule {}

impl SingleReplacementRule for FilterProjectTransposeRule {
    fn rule_type(&self) -> OptRuleType {
        OptRuleType::TopDown
    }

    fn apply(&self, query_graph: &mut QueryGraph, node_id: NodeId) -> Option<NodeId> {
        if let QueryNode::Filter { conditions, input } = query_graph.node(node_id) {
            if let QueryNode::Project {
                outputs,
                input: proj_input,
            } = query_graph.node(*input)
            {
                let new_conditions = conditions
                    .iter()
                    .map(|c| dereference_scalar_expr(c, outputs))
                    .collect::<Vec<_>>();
                let outputs = outputs.clone();
                let new_filter = query_graph.filter(*proj_input, new_conditions);
                return Some(query_graph.project(new_filter, outputs));
            }
        }
        None
    }
}

Again, we can visualize the effect of this transformation with the following example:

Note that this rule may unzip shared nodes, effectively converting the DAG into a tree. For example, if Project 1 was a shared node (a node with multiple parents), this rule would produce a new projection that is not connected with the original one. In a future post we will see how to do predicate pushdown without unzipping the DAG shape of the plan, for cases where maximizing sub-plan reuse is needed.

Next steps

In this first post, we have shown how the query graph is represented, including its representation for scalar expressions and computed properties. Also, we have implemented two very basic rewrite rules.

In some post in the near future, we will introduce a few more rewrite rules together with the rule application driver, that will combine a set of rules in the same traversal of the graph until the query graph reaches a fix point where no further rewrites can be applied.